| 引用本文: | 许贤泽, 宋明星, 龚勇兴, 徐逢秋, 王递进, 隋博文, 郭清泉. 基于扰动补偿的磁悬浮转台分数阶滑模控制[J]. 西南交通大学学报, 2024, 59(4): 766-775. doi: 10.3969/j.issn.0258-2724.20230412 |
| 摘 要: | 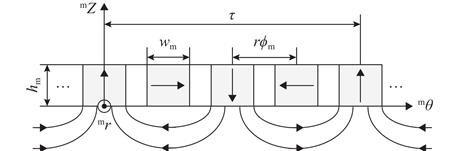
针对存在非线性、耦合性和不确定性的磁悬浮转台的高精度运动控制问题,提出一种基于非线性干扰观测器的分数阶滑模控制方法以提高跟踪精度. 首先,基于系统电磁力模型和动态解耦方法,构建六自由度磁悬浮转台系统动力学模型;其次,设计非线性干扰观测器,对包含系统误差、六自由度间耦合项和外界干扰的集总扰动进行估计,证明了估计误差有界且可调节到任意小;然后,在离散域提出了一种分数阶滑模面,采用分数幂函数替代传统符号函数来抑制抖振,引入分数阶微积分来减小跟踪误差;最后,设计有限时间收敛的分数阶滑模控制策略,并利用李雅普诺夫稳定性理论证明闭环系统稳定性. 实验结果表明:与整数阶滑模控制方法相比,采用所提方法,2个水平自由度和绕竖直方向旋转自由度对三角波的跟踪误差均方根分别减小了12.8%、16.8%和23.7%,最大跟踪误差分别减小9.26%、13.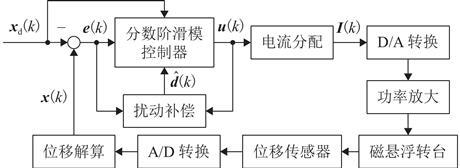
00%和33.20%;跟踪圆形轨迹时,2个水平自由度的跟踪误差均方值分别减小6.39%和12.40%,最大跟踪误差分别减小9.90%和12.10%.

|



