基于改进低秩矩阵补全的交通量数据缺失值插补方法

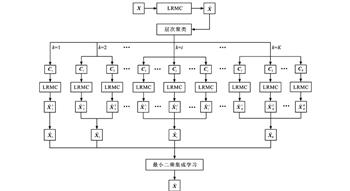
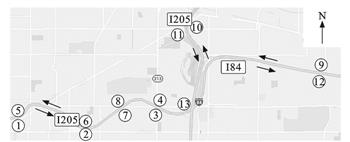
提出了一种低秩矩阵补全的改进方法以研究道路交通量数据缺失值插补问题。应用基于核范数的低秩矩阵补全对交通量数据矩阵中的缺失值进行第1轮插补; 通过层次聚类算法将交通量数据划分为不同类别, 使得同类中的数据具有较强相关性, 异类中的数据具有较弱的相关性; 在每类样本上应用低秩矩阵补全得到缺失值的第2轮插补; 为了减少聚类数的影响, 提出最小二乘回归集成学习方法将不同聚类数下的插补结果进行融合, 得到最终的交通量数据插补结果; 用美国俄勒冈州波特兰市的交通量数据比较了5种方法的插补误差, 并分析了不同聚类数和距离度量方法的影响。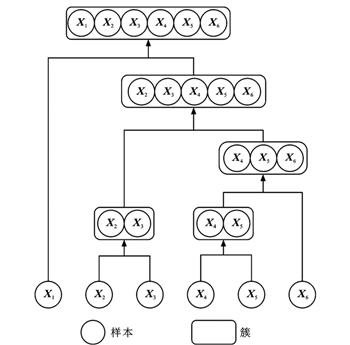研究结果表明: 在完全随机缺失模式下, 缺失率为10%~60%时, 其相对于传统的低秩矩阵补全模型的插补误差降低了5.93%~9.11%;在随机缺失和混合缺失模式下, 插补误差也分别降低了8.32%~9.55%和8.14%~9.20%;集成不同聚类数下的多个插补结果比单一聚类数下的插补误差降低2.62%~4.76%。可见, 在3种数据缺失模式下, 改进低秩矩阵补全方法降低了交通量数据的插补误差, 能有效提高插补后交通量数据的有效性。

Interpolation method of traffic volume missing data based on improved low-rank matrix completion

An improved low-rank matrix completion method was proposed to study the interpolation problem of road traffic volume missing data. The missing data in the traffic volume data matrix were interpolated in the first round by the low-rank matrix completion based on the nuclear norm. Hierarchical clustering algorithm was applied to classify traffic volume data into different clusters so that the data in the same cluster had strong correlation, while the data in different clusters had weak correlation. Low-rank matrix completion method was applied to each cluster to complete the second round interpolation for missing data. In order to reduce the impact of clustering number, the least square regression ensemble learning approach was proposed to combine the interpolation results under different clustering numbers, so as to obtain the final traffic volume data interpolation results. The interpolation errors of five methods were compared based on the highway traffic volume data in Portland, Oregon, USA, and the influences of different clustering numbers and distance metrics methods were analyzed. Analysis result shows that under the completely random missing pattern, when the missing rate is 10%-60%, the interpolation error reduces by 5.93%-9.11% compared with the traditional low-rank matrix completion model. Under the random and mixed missing patterns, the interpolation errors reduce by 8.32%-9.55% and 8.14%-9.20%, respectively. The integration of multiple interpolations under different clustering numbers can reduce the interpolation error by 2.62%-4.76% compared with the results under single clustering number. Therefore, under three data missing modes, the improved low-rank matrix completion method can reduce the interpolation error of traffic volume data effectively, and improve the effectiveness of traffic volume data after interpolation.