曲轴动压滑动轴承非线性油膜力解析方法

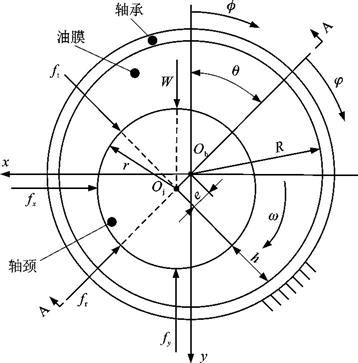
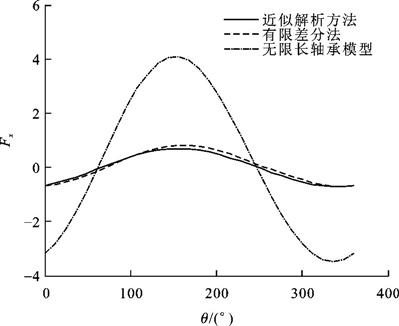
基于分离变量法、Sturm-Liouville理论与下游Reynolds边界条件, 提出了一种求解曲轴动压滑动轴承非线性油膜力的解析方法; 将轴承不可压缩流体动压润滑Reynolds方程的压力分布表示为特解加通解的形式; 运用分离变量法, 将油膜压力分布的特解和通解分别表示为周向分离函数和轴向分离函数相加和相乘的形式; 为了便于求解, 对油膜压力特解的周向分离函数进行Sommerfeld变换, 通过连续性条件确定油膜的终止位置角; 由于油膜压力通解的周向分离函数没有直接解的形式, 通过油膜厚度的逼近函数将油膜压力通解的周向分离函数转化为Sturm-Liouville型方程, 根据边界条件求得本征值和本征函数系, 通过三角函数的无穷级数展开表示油膜压力通解的周向分离函数; 采用含本征值的双曲正切函数表示油膜压力通解的轴向分离函数; 在润滑油膜的完备区域, 对油膜压力分布的解析表达式进行积分, 求得曲轴轴承的非线性油膜力。分析结果表明: 采用解析方法计算的非线性油膜力与有限差分法的计算结果吻合较好, 偏心率较小时非线性油膜力仅相差约5%;当轴承偏心率由0.2增大到0.6时, 油膜终止位置角的最大值减小了13.5%;当量纲为1的速度扰动由0增大到0.03时, 油膜终止位置角变化了3.3%;当本征值的个数不小于20时, 量纲为1的径向、切向通解油膜力的变化较小, 取值分别保持在-2.8、4.6附近。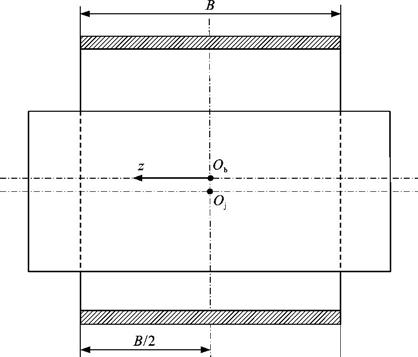由此可见: 采用解析方法能够准确求解曲轴动压滑动轴承的非线性油膜力; 轴承偏心率对油膜破裂的影响较大, 且偏心率较大时油膜易破裂; 相对于轴承偏心率而言, 速度扰动对油膜破裂的影响较小; 当本征值的个数不小于20时, 油膜压力通解的计算精度较高, 能够满足工程需要。

Analytical method of nonlinear oil film force of hydrodynamic crankshaft journal bearing

An analytical method was proposed for calculating the nonlinear oil film force of hydrodynamic crankshaft journal bearing based on variables separation method, Sturm-Liouville theory, and Reynolds boundary conditions.The oil film pressure distribution of Reynoldsequation for incompressible fluid hydrodynamic lubrication of the bearing was expressed as an additive form of a particular solution and a homogeneous solution.By using variables separation method, the pressure distributions of particular solution and homogeneous solution were respectively split in an additive and multiplicative forms of circumferential separation function and axial separation function.For convenience, the circumferential separation function of particular solution was solved by using the Sommerfeld transformation, and the termination position angle of oil film was determined by using the continuity condition.Because there was no direct solution for the circumferential separation function of homogeneous solution, the circumferential separation function was transformed as Sturm-Liouville equation by using the approximation function of oil film thickness, and the eigenvalues and eigenfunctions were obtained by using the boundary conditions.The circumferential separation function of homogeneous solution was expanded by using the infinite series of trigonometric functions.The axial separation function of homogeneous solution was obtained by the hyperbolic tangent function with the eigenvalues.In the complete oil film field, the analytical expression of oil film pressure distribution was integrated to obtain the nonlinear oil film force of crankshaft bearing.Analysis result shows that the nonlinear oil film force calculated by the analytical method is good agreement with the value calculated by the finite difference method, and the difference is about 5% when the eccentricity ratio is small. When the eccentricity ratio rises from 0.2 to 0.6, the maximum value of termination position angle of oil film reduces by 13.5%. When the dimensionless speed disturbance rises from 0 to 0.03, a relative variation of 3.3% is obtained for the termination position angle of oil film.When the number of eigenvalues is greater than 20, the variations of homogeneous solutions of dimensionless oil film force in the radial and tangential directions are really small, and their values are about-2.8 and 4.6, respectively.Therefore, the analytical method can calculate the nonlinear oil film force of hydrodynamic crankshaft journal bearing accurately.The eccentricity ratio has a great influence on the rupture of oil film, and the rupture easily takes place when the eccentricity ratio is bigger.Compared with the eccentricity ratio, the speed disturbance has less influence on the rupture of oil film.A high calculation precision can be obtained for the homogeneous solution of dimensionless oil film force when the number of eigenvalues is not less than 20, which meets the requirement of engineering.18 figs, 25 refs.